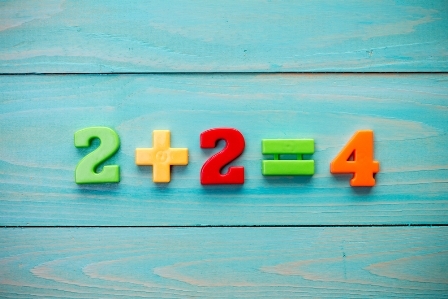
Dr. Howard Gardner on Truth
 ALBUQUERQUE, NEW MEXICO (ANS – May 16, 2018)—During my teacher training days I became familiar with the research and writings of Dr. Howard Gardner. As author of the 1983 book, Frames of Mind: The Theory of Multiple Intelligences, Gardner’s work was mandatory reading for my credentialing program at Chapman University. His insight into how people learn was—and still is—considered imperative for understanding the ways in which people absorb, discover, and engage the world.
ALBUQUERQUE, NEW MEXICO (ANS – May 16, 2018)—During my teacher training days I became familiar with the research and writings of Dr. Howard Gardner. As author of the 1983 book, Frames of Mind: The Theory of Multiple Intelligences, Gardner’s work was mandatory reading for my credentialing program at Chapman University. His insight into how people learn was—and still is—considered imperative for understanding the ways in which people absorb, discover, and engage the world.
At the time (1990’s) there were seven criteria: music-rhythmic, visual-spatial, verbal-linguistic, logical-mathematical, body-kinesthetic, interpersonal, and intrapersonal. Since my stint in the credential program an eighth ability was added: naturalistic. The seven criteria guided how we developed our lesson plans and approached every student. I’m still a big fan of his work and research, referring to it often in a host of different settings. In the world of education, Gardner casts a long shadow; he’s very influential.
Every now and then I’ll pick up another book to read by Gardner. Since my doctorate work was in educational philosophy (an emphasis in 1st century education leading to the Middle Ages), I’d take a peek to see what Gardner had to say about certain topics. And though I finished my graduate studies prior to the release of his book Truth, Beauty, and Goodness Reframed: Educating For the Virtues In the Age of Truthiness and Twitter, I made sure I picked up a copy because the topics he discussed—truth, beauty, and goodness—we important in my research and field of study [1].
 Gardner does a decent job summarizing truth, beauty, and goodness, known as the transcendentals in philosophy [2], putting them within the context of our contemporary world. I love the fact that he’s an advocate for them, seeing them as necessary ingredients for life and education. But as expected with someone coming from a theistic worldview, I’d disagree with a several of his statements. And for the sake of this short article I’ll highlight one.
Gardner does a decent job summarizing truth, beauty, and goodness, known as the transcendentals in philosophy [2], putting them within the context of our contemporary world. I love the fact that he’s an advocate for them, seeing them as necessary ingredients for life and education. But as expected with someone coming from a theistic worldview, I’d disagree with a several of his statements. And for the sake of this short article I’ll highlight one.
In the chapter on Truth Gardner examines humanities pursuit of truth, noting its fickle nature, particularly in our post-modern era where truth is bent, re-arranged, and denied on multiple levels (so much so since the publication of the book in 2011). Gardner defines truth as “essentially a property of statements, of propositions…” Gardner understands truth is found in science, particularly physics and mathematics. Gardner states, “The firmest set of truth lies in mathematics: 2 + 2 = 4, and so long as one remains within the realm of arithmetic, this truth will not change.” Gardner infers mathematical truth is set—“will not change,” barring a new understanding of mathematics such as non-Euclidean geometry or, I’d add, Kurt Gödel’s Incompleteness Theory. So on a basic level, Gardner recognizes that there is, what I’d call, micro-truth; there is some type of truth to be discovered.
It might be good to pause and ask an obvious question: what is Gardner’s understanding of truth? Generally speaking, there are four theories of truth: correspondence (truth is what corresponds to reality), inflationary (truth is referring to propositions), coherence (truth coheres with propositions), and deflationary (affirmations of truth). So though Gardner doesn’t specify his school of thought, the definition he provides aligns itself with inflationary theory, truth as properties of propositions. In an article like this, I don’t have time to unpack these differing theories. I’d direct your attention to David Agler’s article [3]. But for the sake of this critique, I will go with Gardner’s inferred meaning: truth as metaphysical realism, i.e math, something things that can be verified through logical propositions and processes (equations, formula, etc.). In short, math discovers truth (others would say creates truth), aligning to the way things are in the world. And if this is the case, if one can discover that 2 + 2 = 4 is true, we should be able to discover other truths using mathematics, correct?
 To answer the question, some people would argue that any model within mathematics that satisfies Peano’s Axioms is generally valid, therefore true. And as physicists show, there are phenomena that satisfy a basic understanding of how things work, consistent with the world. As an example: the laws of physics (gravity, motion, conservation, mass, energy, etc., all involving math). These principles and properties are actual and factual: they exist, are observable, measurable, and consistent. This said, mathematics and physics are a type of micro truth; they correspond to how things are. And even though we don’t fully comprehend the quantum world, I think it’d be safe in saying that the quantum world exists, it’s real, and works in accordance with certain principles, a type of quantum truth we’ve yet to fully comprehend. My point with this brief discussion is this: truth exists, at least on the micro-level; there are certain things that relate and agree with reality, from the broad world of arithmetic and physics to the small world of quantum mechanics. I think Gardner would agree with me.
To answer the question, some people would argue that any model within mathematics that satisfies Peano’s Axioms is generally valid, therefore true. And as physicists show, there are phenomena that satisfy a basic understanding of how things work, consistent with the world. As an example: the laws of physics (gravity, motion, conservation, mass, energy, etc., all involving math). These principles and properties are actual and factual: they exist, are observable, measurable, and consistent. This said, mathematics and physics are a type of micro truth; they correspond to how things are. And even though we don’t fully comprehend the quantum world, I think it’d be safe in saying that the quantum world exists, it’s real, and works in accordance with certain principles, a type of quantum truth we’ve yet to fully comprehend. My point with this brief discussion is this: truth exists, at least on the micro-level; there are certain things that relate and agree with reality, from the broad world of arithmetic and physics to the small world of quantum mechanics. I think Gardner would agree with me.
But others may not. Here’s how one mathematician posed the problem:
“For example, 2 + 2 = 4 can be a subjective truth, but in order for it to apply in any meaningful way to objective reality, it must be proven absolutely that objective reality contains differing quantities or values (generally an intuitive given). Does it? Probably, but would a photon think so? To a photon the universe is a singularity, talking about 1 + 1 = 2 would make no sense to the photon, to which only 1 exists. Who is right? If the answer is both, it is not a universal truth as both descriptions of the universe are mutually exclusive, and 2 + 2 = 4 is not necessarily true” [4].
Though a complete dissection of this statement is needed to address its various nuances, it is the question and answers given by the mathematician I draw your attention: “Does it? Probably…” Even when dealing with quantum objects we don’t completely understand—the photon, the answer to the question does 2 + 2 = 4 is “probably” (aka most likely or undoubtedly). Why? It best describes reality; it describes the way things are. Even with skepticism stated, “not necessarily true,” the mathematician recognizes that there is a type of basic truth, “probably.” So does 2 + 2 = 4? Yes, logic, clear thinking, and commonsense mandates recognition of the answer. And for all intents and purposes, math provides the closest physical approximation to truth. So I’d agree with Gardner as related to physical truth: math is “the firmest set of truth…”
To this point I think we can settle on this: truth exists, at least micro truth: truth specific to a certain properties or reality.
 But here’s my problem: a few pages later Gardner states, “To be sure, there is no single truth and certainly no absolute truth.” “No single truth?” This statement is in direct conflict with his prior statements concerning mathematics, things that present a single truth—math. And if this is the case—“there is no single truth”—then Gardner’s statement is meaningless; it is self-defeating. His statement “there is no single truth” is a truth claim, but if single truth doesn’t exist, then his claim can be dismissed; it’s not true. Not to mention the hundreds of other truth claims made in his corpus of books. And if his definition of truth as a “property of statements, of propositions” stands, all his statements and propositions are untrue, that is, if truth doesn’t exist.
But here’s my problem: a few pages later Gardner states, “To be sure, there is no single truth and certainly no absolute truth.” “No single truth?” This statement is in direct conflict with his prior statements concerning mathematics, things that present a single truth—math. And if this is the case—“there is no single truth”—then Gardner’s statement is meaningless; it is self-defeating. His statement “there is no single truth” is a truth claim, but if single truth doesn’t exist, then his claim can be dismissed; it’s not true. Not to mention the hundreds of other truth claims made in his corpus of books. And if his definition of truth as a “property of statements, of propositions” stands, all his statements and propositions are untrue, that is, if truth doesn’t exist.
As one can see, there’s an incongruity with this type of thinking. Gardner states that 2 + 2 = 4 is a type of truth, but then says there is no “single truth.” So is 2 + 2 = 4 not true? It seems to me as though Gardner wants to have it both ways: to have truth and no truth at the same time. But there’s an issue: either 2 + 2 = 4 or it doesn’t. It can’t be true and not-true at the same time. The law of non-contradiction must be followed or a disruption of cogent thinking will ensue. The Law of Non-contradiction states that something cannot be both true and false at the same time. If you pay for an item that was $2.00 with a five $5.00 bill, and I give you $1.00 in change, you’d say my math is off (aka…the truth of my numbers/calculation is wrong). And if I say 5 – 3 = 1, you’d scream that it is not, it’s a contradiction of basic math. The answer is 2. Why? Because there’s a correct number to the equation, a single truth to a particular problem, there is a right answer. My point: it’s difficult to argue against non-contradiction in the realm of numbers and logic. Math cuts to the truth unlike most things; it corresponds to the way things are in reality, both physically and metaphysically (number are, after all, metaphysical properties). Something is either true or it’s not true; there’s truth—micro, macro, or otherwise—or there isn’t. So if numbers, propositions (logic), and formula axioms can be true, then truth exists, at least on a single, micro-level.
Here’s my parting thought: if micro-truth can be discovered (such as mathematics or physics) why not macro-truth? If individual parts are discovered, why not the whole? Put another way, if truth exists with basic things such as arithmetic, why not with broad things such as absolutes? I’m not claiming science, history, math or anything else has given us the complete picture of physical truth to this point (the elusive theory of everything), but to deny truth is to deny existence. And when all is said we at least know one thing: something exists; I exist; there is being. And this statement (I exist) is a truth claim verified by reality, actuality. So if a micro truth is possible—I exist, there is being, then a macro truth is probable; the part speaks to the whole. So at its basic level Gardner’s statement “There is no single truth and certainly no absolute truth” would have to untrue to be true, leading to a contradiction.
I’m glad Howard Gardner believes in some type of truth (math), for believing in part, points to a probable whole. Further, I’m glad he’s not a consistent truth-denier. For if he was we couldn’t find any truth in his deep thought. Luckily, we can. In recognizing the need for truth, beauty, and goodness (lower case) in life and education, Gardner, whether he wants to acknowledge it or not, is saying there is Truth, Beauty, and Goodness (capitalized) to be discovered. And incongruity of his thought aside, I would agree with him: Truth, Beauty, and Goodness is real and relevant to our world today.
- The Master Teacher, 2004, 2007.
- A quick word is in store on the three words—truth, beauty, and goodness, known as the transcendentals in philosophy, and designated as virtues by Gardner. The transcendentals have been part of human for thousands of years as the written records indicate; all cultures have dealt with them on one level or another. In the West, Plato, Pythagoras, Socrates, and Aristotle all had something to say about the transcendentals. During the first century, Paul of Tarsus interwove the transcendentals in a broader context, best portrayed in his letter to the Philippians, chapter 4:8. In the Middle Ages thinkers such as Plotinus, Pseudo-Dionysius, and Augustine weighed in on the areas. And Thomas Aquinas helped broaden our understanding of truth, beauty, and goodness as it relates to theology. But in our contemporary world the transcendentals have been separated. As an example, truth has been relegated to the sciences, beauty to the arts, and goodness to religion. But historically, they are not separate entities, but one, all leading back to metaphysical principles, ontology and being. Generally, humanity sought the transcendetals as a means to understand and appreciate life, asking what is true, how is something beautiful, and what does it mean to live a good life?





